GSD and how to calculate it
August 26, 2020
by Kevin McDonough
What is GSD?
GSD stands for Ground Sample Distance. It is, essentially, the size of a camera frame pixel in the real-world. This is an essential element of performing UAS based inspections because it allows us to measure image frame objects in the real world. That is, the size of an object in an image can be measure by its width and height in pixels which can then be translated into a physical distance using the GSD. As an example, assume you have a square object that is 10 pixels wide and 12 pixels tall and an image GSD of 5 cm per pixel. Then the object would be 50 cm wide and 60 cm tall in the real world.
If the camera sensor has square pixels (which is the case for many commercially available camera sensors), the GSD in the image can be thought of the real-world distance between two consecutive pixel centers. Or, more simply, the length of on of the pixel edges (the length d in Figure 1).

Figure 1. GSD in an image
Calculating GSD?
Calculating GSD can be pretty straight-forward when the object being captured is close to parallel with the lens, see Figure 2. In this figure, we have a camera looking straight down at the ground (though the whole thing is laying on its side). We see the similar triangles from the lens to the camera sensor and from the lens to the ground. The distance from the lens to the camera sensor is the camera focal length, f, and the distance between the lens to the ground is the altitude of the camera, h.
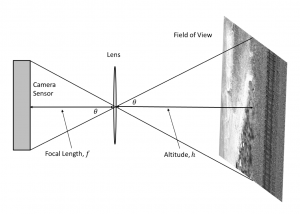
Figure 2. Diagram of important camera and image elements used for GSD calculation.
Because of the similar triangles, we can easily estimate the GSD assuming we know the following three things:
- The altitude (or range) of the camera to the target object, h.
- The focal length of the camera when the picture was taken, f.
- The size of a side of a pixel in the camera sensor (assuming square pixels), d.
The GSD is then estimated as
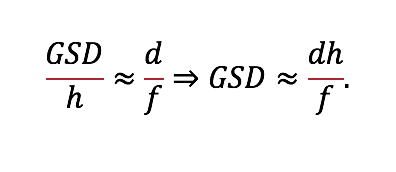
This analysis is meant to teach with an intuitive example what GSD is and how to calculate. For more complicated examples, these principles remain the same, but the details get more complicated.
